FAJ：赋予自由，实现最优

　　炒股就看金麒麟分析师研报，权威，专业，及时，全面，助您挖掘潜力主题机会！

　　来源：北京金融分析师协会

　　* 此项目由CFA Institute及CFA Society Beijing联合推出。

　　The Financial Analysts Journal 创刊于1945年，是CFA Institute主办的投资管理领域专业期刊。2020年，该刊位于社会科学引文索引（SSCI）二区。本中文推介项目得到了FAJ编辑部的授权。

　　FAJ： 赋予自由，实现最优

　　3D Investing： Jointly Optimizing Return， Risk， and Sustainability

　　作者：David Blitz， Mike Chen， Clint Howard， and Harald Lohre

　　推荐语：白雪石，CFA

　　翻译：刘泽超，CFA

　　校审：白雪石，CFA

　　原文链接：Financial Analyst Journal，Vol.80，Issue 3 （ 点击文末“阅读全文”可查看 ）

　　推荐语

　　本文来自Robeco公司首席研究员David Blitz，创新研究负责人Mike Chen，量化研究员Clint Howard，量化股票研究负责人Harald Lohre。

　　1952年，哈利·马科维茨开创的现代投资组合理论，让投资从“口口相传”的技艺成为高度理性的科学。随着1965年威廉·夏普将此理论作为市场上所有投资者组合构建的前提假设，CAPM模型揭示了市场更加简洁优美的微观结构，“马-夏”合璧生辉，似乎一条现代投资组合理论的康庄大道已在眼前，既能解释过往，又能筹划未来，从大类资产配置到组合管理实践，从市场价值发现到套利均衡实现，无所不包。研究与实践者要做的，无非就是陈述自身风险偏好、量化组合约束条件，在“马-夏大道”上圈地跑马。

　　然而，任何伟大的历史道路，也很可能是走向分叉的十字路口。对预期回报μ和预期风险矩阵Σ——“马-夏大道”的两颗明珠的研究与运用，正是从此时走上了不同的道路。

　　如果我们上溯历史之河，我们会对更加体会到两颗明珠的来之不易。3000年前，犹太人在《塔木德》中所谓“1/3土地，1/3生意，1/3储蓄”的教条，本质是0维的，它没有任何寻求优化的努力，只是安于经验法则的现状，因此也不需要纳入任何决定组合表现的努力；直到100年前，本杰明·格雷厄姆开创的价值投资理念才创世般实现了“从0到1”的突破，“投资价值”成为决定最优配置目标的唯一维度，而其中蜷曲着的μ和Σ则又过了50年才被发现并获得了自由。

　　“马-夏”合璧以来，致力于对预期风险矩阵Σ研究与实践者，并未在市场因子β面前止步，他们选择对“风险”予以更多自由、包容和探索性的定义和刻画，更多的决定证券收益的风险因子被一一释放出来，多因子模型开枝散叶，一木成林，蓬勃自由，最终奠定了以因子投资为基础的现代量化投资理论的基石。

　　反观对预期回报μ的研究，则一直处于高度压抑的状态，财务收益率仍然被作为唯一的“回报”维度来解读，日趋复杂的资本市场假设都是为了更好的刻画预期的财务收益率，至于投资者本来早就面临的各种现实约束，都通通不被视作目标，而是全部打包扔进约束条件的不等式当中。

　　但是，当这些人试图在ESG可持续投资当中，使用同样的“打包”行为继续简单粗暴的使用约束条件不等式的时候，本文作者David Blitz及其团队做出了不同的选择，并很可能开创新的思潮：将ESG可持续投资目标得分μSI与财务收益率μ并列，共同进入到优化目标函数而非约束条件当中。

　　这个变化看似微小，却是一个60年来都不曾发生的改变。追求投资回报，却从未追问过“回报”的内涵有哪些？以“约束”的名义，让大量的回报目标丧失了自由，蜷曲在低维的世界里，这不应该马科维茨的初衷。我们知道，之所以他的理论冠以“现代”二字，是因为其理论体现着追求理性、赋予自由的现代性精神；他开创的道路当然也可以分叉，因为他也曾如摩西般为金融研究与实践者开海为路，带他们走出蛮荒，进入金融市场的理性自由之域。

　　以此纪念60年前的那一次投资理念的分叉，那是一次伟大的分道扬镳；而在今日，它再度发生。

　　“相逢不可欺，偶然如飘蓬。于道各努力，千里自同风。”

　　摘 要

　　传统均值方差投资组合优化的前提是投资者只关注回报和风险。然而，一些投资者也有非财务目标，例如可持续发展目标。我们展示了如何将传统方法扩展到均值-方差-可持续性优化，并解释为什么这种3D投资方法是事前帕累托最优。我们在几项研究中凭实证说明了其功效，包括碳足迹和可持续发展目标。重要的是，我们得出了在哪些条件下，3D优化方法优于可持续性约束条件下的2D方法。

　　关键词：碳足迹、ESG、因素投资、投资组合优化、可持续发展目标、可持续投资

　　披露：作者们披露他们受雇于Robeco，这是一家提供各种投资产品的公司。这些产品的构建有时可能会利用与本研究相关的见解。本文中提出的观点和结果并非由Robeco的观点或利益所驱动，也不代表其观点。

　　01 引言

　　标准的回报-风险投资组合框架受到多种方法的挑战，这些方法侧重于根据非严格基于风险或回报的目标做出投资决策，比如影响力投资、社会责任投资（SRI）或环境、社会和公司治理（ESG）投资。这些可持续投资（SI）理念的扩散凸显了标准均值-方差框架（Markowitz，1952年）已不再足够。因此，将可持续性目标纳入投资组合考虑因素中有广泛需求，比如与碳足迹、ESG和可持续性发展目标（SDG）相关的指标。在本文中，我们将多目标投资组合优化框架与替代投资目标的实际实施结合起来。具体来说，我们将使用约束条件将可持续性目标纳入投资组合的常见做法与使用嵌入目标函数的做法进行了比较，并讨论了何时一种方法可能比另一种方法更可取。

　　Sandberg等人（2009年）和Horan等人（2022年）强调了社会责任投资（SRI1）的多样性，指出没有一种适用于所有情况的方法来开发以可持续性为导向的投资组合。文献提出了许多将可持续性目标纳入投资组合的方法。这些方法包括从投资范围中排除不受欢迎的股票（Diltz，1995年；Kinder和Domini，1997年；Naber，2001年），限制投资组合对这些目标的暴露（Boudt， Cornelissen和Croux，2013年），以及将可持续目标纳入目标函数的回报/阿尔法部分（Bilbao-Terol， Arenas-Parra和Canal-Fernandez，2012年；Hirschberger等人，2013年；Utz等人，2014年；Chen和Mussalli，2020年）。然而，关于如何最佳地将可持续性目标纳入投资组合的核心问题尚未得到充分的研究和解决。

　　[1] Socially Responsible Investing

　　投资者通常针对投资组合的碳足迹设定比某个基准更低的目标，或实现比基准更高的SDG得分。2这些目标自然适合于基于约束的框架，因为相对于基准的约束可以很容易地满足这些投资需求。在约束水平较低时（例如仅仅要求比基准好），这种方法可能效果很好。然而，在更宏大的目标下，基于约束的方法面临诸多挑战。Blitz和Hoogteijling（2022）阐释了碳足迹约束可以被解释为隐含碳税（对预期回报）。当约束未起作用时（即多余的），那么税收实际上就是零。但是，当约束起到约束作用，这意味着高碳足迹股票从预期回报的角度来看非常有吸引力，因此约束必须对这些股票施加大量的隐含碳税，以防止优化算法购买它们。我们试图回答的实证问题是，在目标函数中添加可持续性指标（使用多目标优化框架）或通过投资组合约束，是否能够实现更好的投资组合回报和可持续性特征。换句话说，3D投资在同时瞄准可持续性目标和预期回报时是否优于简单的2D方法辅以可持续性约束条件？

　　[2] 投资组合的碳足迹减少（以CO2排放量除以公司规模的某种度量来表示）是最常见的可持续性目标之一。例如，可以参考Andersson， Bolton， 和 Samama （2016）， Hao， Soe， 和 Tang （2018）， Gorgen， Jacob， 和 Nerlinger （2020）， Roncalli 等人（2020）， Bender 等人（2020）， Bolton 和 Kacperczyk （2021）， Bolton， Kacperczyk， 和 Samama （2022）， 以及 Kolle 等人（2022）的研究。

　　我们根据两个相关的实例回答这个问题，即如何将可持续性目标整合到投资组合中。图1显示了在减少碳足迹或提高SDG得分（相对于MSCI世界基准指数）时，实际投资组合的盈亏平衡交易成本如何变化。我们发现，对于碳足迹减少和SDG得分提高，3D投资方法都是优越的解决方案，尤其是在更宏大的可持续性目标下。综合起来，我们的结果表明，对于寻求紧密跟踪基准同时超越基准的投资组合来说，可持续性目标纳入目标函数项（3D投资）优于2D方法辅以约束。

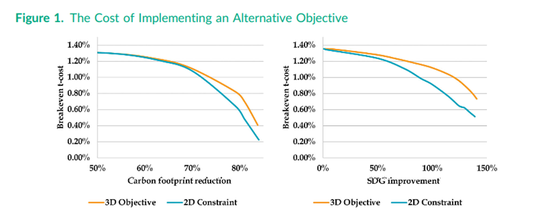
　　这样的结果并不令人惊讶，因为我们使用的3D投资优化框架是事前帕累托最优的（Zadeh 1963）。也就是说，对于给定的预期回报水平、可持续性表现和风险水平，我们的方法能够分别实现最大的预期可持续性表现或预期回报。改善一个特征（预期回报、可持续性或风险）需要在接受其他一个或多个特征的更差结果的情况下进行。帕累托最优性增加了我们方法的理论吸引力，并有助于实现其实际应用中的增值。

　　尽管如此，人们可能会认为可持续性只是一种可以测量并纳入标准均值-方差优化框架风险维度的风险。这当然是一种可能性，其中可持续性的某些要素可以纳入风险模型。然而，由于可持续发展的定义极其多样化（Berg、Kolbel 和 Rigobon 2022），某些可持续发展观点并不完全符合传统的风险或回报考虑。除了风险和回报之外，拥有一个灵活的框架很有价值，可以轻松地合并和归因这些观点。

　　本文涉及大量文献，这些文献扩展了标准均值-方差优化框架以纳入另类投资目标。哈勒巴赫等人（2004）引入了将包含 SRI 偏好等因子纳入传统2D投资组合构建过程的投资决策框架。其他早期的研究成果侧重于将非财务目标整合到投资组合优化过程中所需的优化方法（Bilbao-Terol、Arenas-Parra 和Canal Fernandez 2012；Ballestero等人 2012；Dorfleitner和Utz 2012；Utz等人 2014；Calvo， Ivorra和Liern 2015；Calvo， Ivorra和Liern 2016）。近年来，焦点转向ESG高效投资组合的构建以及这些投资组合如何与标准均值方差有效前沿相关（Chen和Mussalli 2020；Geczy、Stambaugh 和 Levin 2021；Pedersen、Fitzgibbons 和 Pomorski 2021；Schmidt 2020；Shushi 2022；Steuer和Utz 2023；Wu等人 2022；Xidonas和Essner 2022；Alessandrini和Jondeau 2021；Coqueret等人 2021）。我们通过展示这些方法的实际实施的有效性来做出贡献。具体来说，我们展示了所需的投资组合特性如何与将可持续性因素整合到投资组合中的不同方法相互作用。

　　最终，投资组合约束仍然并将继续应用于构建投资组合。在一些情形下，最低投资组合风险敞口或可持续性指标必须持续保持，那么这只能通过约束条件来实现。然而，如果投资者的目标是追求长期平均的可持续性目标和偏差（即短期偏离可以接受），我们的结果表明，3D 投资可以以较低的调仓频率提供满足要求的投资组合，从而获得更高的后期成本效益。此外，当给定股票的预期回报相对特别高时（牺牲小幅可持续性发展目标，获得相对更高预期回报），我们的方法具有灵活性，反之亦然。因此，当预期回报和可持续性特征对投资者都很重要时，我们的3D投资框架可确保预期回报和可持续性的联合最优性。

　　02 多目标优化框架

　　2.1 标准均值-方差优化

　　经典的均值-方差优化问题为：

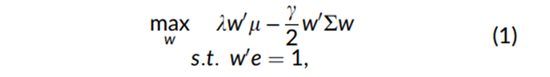
　　其中：w是N*1向量的资产权重，μ是该资产对应的预期回报，∑是一个N×N的方差-协方差矩阵，e是一个 N×1 的全向量，λ和γ是标量系数。根据方程（1）生成的投资组合在均值-方差意义上是最优的，因为它们在给定风险水平下实现了最大预期回报。这个框架可以扩展包括额外维度，比如相对于某个基准约束投资组合（Jorion 2003），纳入交易成本惩罚（Taksar， Klass和Assaf 1988； Ledoit和Wolf 2022），惩罚调仓频率（Hautsch和Voigt 2019），或者强制资产权重为正（Jagannathan和Ma 2003）。

　　2.2 多目标优化框架

　　等式（1）中的均值-方差优化可以直接扩展为在三个（或更多）维度的有效前沿面上构建投资组合。即，在考虑可持续性的情况下，方程（1）可以推广到三个维度：

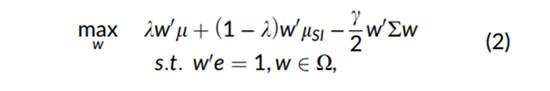
　　其中：μSI是N*1向量的可持续发展指标；λ变成了在回报和可持续发展指标间的相对偏好；Ω是可行解的集合，考虑了所有投资组合的限制条件。这个方程可以容纳可持续性特征。比如：来自诸如MSCI和Sustainalytics等供应商的商业 ESG 指标、碳足迹、SDG得分和气候转型分数，可持续性指标应是序数数据。

　　这种多目标优化技术称为加权和方法（Marler 和 Arora 2010；Stanimirovic、Zlatanovic 和 Petkovic 2011），所得解决方案可以证明是帕累托最优（Zadeh 1963）。该技术允许在多维有效前沿表面上构建投资组合。此前，这种类型的投资组合构建已应用于投资实例，如 Gintschel和Scherer （2004）、O’Cinneide、Scherer 和 Xu （2006）、Ballestero等（2012）、Dorfleitner 和Utz（2012）、Calvo、Ivorra和Liern （2015）、Chen和Mussalli （2020） 以及Steuer和Utz （2023）。我们在后续的实证分析中采用了这个 3D 投资框架，重点关注将“碳足迹减少”和“SDG得分改进”纳入基准相关的投资组合优化设置中。尽管我们聚焦于两个特定的可持续发展指标（碳足迹减少、SDG得分改进），但所提出的框架可推广到任何可以表示为一系列离散或连续值的序数度量。

　　03 数据及方法论

　　3.1 数据

　　我们的样本由1989年12月至2022年12月每个月末的MSCI全球成分股组成。我们从 Refinitiv获取股票收益和基本面数据。继 Blitz 和 Hoogteijling（2022）之后，我们通过将范围1和范围2碳排放量（来自Trucost的数据）3 除以包括现金在内的企业价值 （EVIC） 来计算股票的碳足迹。Busch、Johnson和Pioch （2020）指出，不同数据供应商的企业碳数据质量可能存在差异，特别是在估计数据点方面。当我们从MSCI范围构建投资组合时，我们需要足够的数据覆盖范围。因此，我们在可用的情况下使用公司报告的数据，在数据缺失的情况下使用Trucost估计的数据。EVIC的计算方式为公司股票的市场价值加上其债务的账面价值。我们从 MSCI 获取股票级别的ESG分数，数据从2009年1月开始。我们从Robeco获取 SDG 分数（Van Zanten 和 Huij 2022），这些是七个离散变量，介于-3和3，衡量公司对 SDG 的贡献。对于碳足迹、ESG分数和SDG分数，缺失数据用横截面全球行业分类标准 （GICS） 子行业（2 级）中位数填充。

　　【3】 ISO标准：范围1和范围2都是组织运营过程中产生的排放，范围1是直接排放，范围2是间接排放。

　　在随后的实证分析中，我们提出了通过多目标优化与约束来对比投资组合构建方法的结果，其中我们的目标是减少碳足迹和改善SDG得分。请注意，我们故意选择不报告MSCI ESG改进的结果。这一决定是由于近年来MSCI ESG评分的偏斜分布（Skewed distribution）和集中度所致。这种不断变化的分布，无论是否有经验依据，都使得将各自的可持续发展目标纳入相对于基准的投资组合优化框架变得具有挑战性。变化的分布需要更改约束和目标函数项的参数，从而进一步增加优化问题的复杂性。在介绍过碳足迹和可持续发展目标分数的3D投资结果后，我们将再次审视此类不断变化的可持续发展数据的投资影响。

　　3.2 投资组合优化

　　我们使用投资组合优化设置来模拟现实中投资组合的构建，应用现实的投资组合约束和设置。我们寻求构建跟踪误差在0.5%至1.0%范围内的投资组合，因为这代表了具有挑战性的多目标场景——以有限的风险预算实现高预期回报和可持续发展目标。因此，所使用的设计参数反映了这些较低跟踪误差的组合目标。投资组合对地区（定义为北美、欧洲和亚太地区）和 GICS 第一层级行业4 的敞口限制为基准市值加权值的±0.5%。投资组合权重必须为非负（即仅做多）。最大交易规模限制为股票过去65个交易日日均交易量的 25%。相对于基准的最大股票权重（即活跃权重）为±0.5%。投资组合的最大活跃份额为40%。投资组合的总敞口必须为100%（即全额投资）。我们假设管理的基金随着实现的市场回报而增长，我们设计的模拟为至2022年底的最终基金规模为40亿欧元。我们将调仓惩罚纳入目标函数，即绝对交易规模的平方和。

　　【4】GICS（全球行业分类标准，Global Industry Classification Standard）level one sector指的是GICS体系中的第一层级，即“经济部门”或“行业板块”，包括11个经济部门。

　　由于我们设定跟踪误差，我们将方程（2）中的权重向量从绝对资产权重改为基准相对权重：

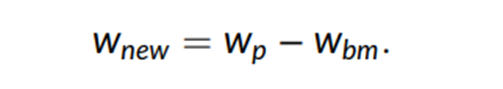
　　我们序列中的单个数据点投资组合优化问题由下式给出：

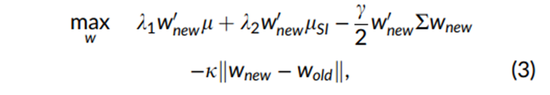
　　Wold表示投资组合在重新平衡之前的权重，κ是用于衡量换手率惩罚的缩放参数（我们设定 κ = 1），并且我们加入了之前描述的约束条件。我们在模拟中使用一组基础的投资组合构建约束和设置，然后对预期回报系数λ1、风险厌恶系数γ和可持续性系数λ2进行不同的优化调整。最后，我们引入了一个额外的可选约束，可以是碳足迹或可持续发展目标（SDG）得分（例如，投资组合的碳足迹必须小于或等于基准碳足迹）。

　　3.3 预期收益与风险

　　作为预期回报率值μ的输入，我们使用一个简单的等权重多因子评分（记作 QMV5 ），它由质量（Quality）、动量（Momentum）和价值（Value）组成。对于价值，我们使用P/B和12个月前瞻性P/E的等权重组合，并在GICS（全球行业分类标准）行业内部进行排名；对于质量，我们使用资本回报率（Return on Equity）和资产负债率（D/A）的等权重组合。对于动量，我们使用前（12-1）月的回报率。这四个底层信号首先在-1到+1之间进行标准化排名。然后将这些信号组合成一个单一的多因子评分。我们的目标不是构建最好的多因子评分，而是构建一个简化的评分，它代表了多因子投资策略的常见选择和实施方式。

　　【5】Quality， Momentum， and Value multifactor strategy

　　表1分别列出了基于如下维度进行投资组合排序后的独立结果：（1）可持续性得分（Carbon Footprint、ESG和SDG）；（2）质量、动力和价值信号；以及（3）QMV。每个月末，我们将股票组合按照排序分为五组投资组合，并展示持有投资组合一个月所获得的最高和最低五分之一投资组合之间的回报差。表 1的A面板展示了标准投资组合统计数据，B面板展示了这些顶部减去底部的投资组合回报之间的相关性。我们可以观察到可持续性得分往往具有较低的顶部底部回报差和较低的α（相对于市场回报），同时我们看到质量、动量和价值等因素具有显着的资本资产定价模型（CAPM）α和高夏普比率。从相关性角度来看，我们观察到质量、动量和价值之间一致且正相关，而可持续性得分与QMV之间的相关性接近于零。这凸显了这些选定的可持续发展措施与典型的预期回报措施相比具有差异化特质。

　　关于预期风险，我们使用标准的方差-协方差矩阵（∑），它遵循一个潜在因子模型方法，其中我们对样本方差-协方差矩阵应用主成分分析（PCA）并使用20个成分，这个样本方差-协方差矩阵是基于60个月的日回报数据估计得出的。我们使用五天重叠回报来考虑市场异步性（Burns、Engle和Mezrich 1998；Martens 和Poon 2001）。

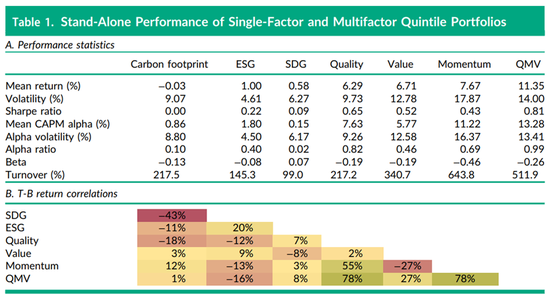
　　注：该表展示了可持续性指标、投资因素和QMV投资组合的单变量顶部减底部 （T-B） 投资组合统计数据。ESG的样本为2009年12月至2022年12月，所有其他结果的样本为 1989年12月至2022年12月。根据每个特征将股票分类为五等分投资组合，每月重新平衡并持有一个月。A面板报告了T-B投资组合的年化绩效统计数据。Alpha是通过将T-B投资组合回报率回归到超过无风险利率的市场回报率来计算的。调仓率是年化单向投资组合调仓率（比如，每月完全替换顶部和底部的投资组合，则对应全年值为2，400%）。B面板报告了 T-B 投资组合回报系列的相关性。

　　ESG=环境、社会和公司治理；QMV =质量、动力和价值多因素策略；SDG=可持续发展目标；CAPM=资本资产定价模型。

　　04 实证结果

　　4.1 均值-方差-可持续性前沿

　　在构建长期的完全优化投资组合前，我们首先计算预期回报、风险和可持续性的事前观点。传统2D有效边界（线）转变为3D有效面板（面）。图2显示了截至2022年12月的跟踪误差、预期回报和碳足迹（相对于基准值）之间的事前3D有效表面。表面颜色从绿色（碳足迹低于基准）到品红色（碳足迹高于基准）。我们还绘制了简单的二维均值方差有效前沿（黑色实线）。我们观察到第一个重要结果，即“绿色”区域和“品红色”区域之间的表现差异。在绿色区域中，对于给定的跟踪误差，更高的预期回报需要牺牲碳足迹减少（面板朝向读者方向）。在品红色区域，对于给定的跟踪误差，我们通常观察到随着预期回报的增加，碳足迹的减少保持恒定（即，表面的形状与典型的均值方差有效边界相似）。这一结果凸显了在给定的碳足迹减少水平下，预期回报-跟踪误差有效边界如何变化。

　　图2描绘了3D表面，而图3将事前风险-回报-可持续性有效表面呈现为碳足迹和可持续发展目标分数的趋势线集合。A组显示了标准的“风险回报有效前沿”，其中远离传统“最大风险回报有效前沿”的每个额外边界点都对应于更高的可持续性目标。B组呈现了“风险-可持续性有效前沿”，其中每个额外边界点都对应于更高的预期回报目标。一般来说，对于碳足迹减少和可持续发展目标改进，随着期望的可持续目标或预期回报目标的增加，可实现的有效边界分别远离最大风险-回报或风险-可持续性有效前沿。因此，在不导致跟踪误差显着增加或预期回报显著减少的情况下，存在投资组合碳足迹降低空间。例如，在跟踪误差为2%的情况下， 0%和60%的碳足迹减少实际上不存在预期回报差异。然而，为了提高SDG 分数，任何高于基准水平的改进通常都需要牺牲预期回报或增加事前跟踪误差。

　　图2和图3的结果表明，在跟踪误差较低的情况下，如果想要显著提高投资组合的可持续性，通常需要牺牲预期回报。随着跟踪误差的增加，风险-回报-可持续性有效面的上限往往更接近最大风险-回报或风险-可持续性有效边界，反映了更多的组合机会。另一种看待这一问题的方法是通过实现给定碳足迹减少所需的最小事前跟踪误差的视角。例如，2022年 12月，碳足迹减少 50%需要事前跟踪误差最小为0.75%左右，而碳足迹减少70%需要事前跟踪误差最小为1.75%。忽略碳足迹和预期回报之间的任何相关性，如果跟踪误差预算为 1.00%，使用0.75%的风险预算来实现所需的碳足迹减少，则可用于承担预期回报风险的风险预算就会减少。但是，如果跟踪误差预算为 5.00%，则您有相对更多的风险预算可用于增加预期回报的敞口，因此更有可能同时满足可持续性和预期回报目标。

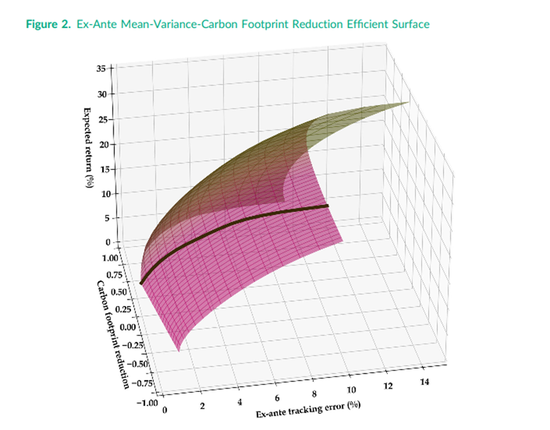
　　注：该图绘制了减少碳足迹的事前预期回报-跟踪误差-可持续性曲面。黑色实线对应于事前预期汇报-跟踪误差有效边界。该曲面根据y轴变量（相对于基准的碳足迹减少量）进行着色，其中绿色对应于较高的减少量，品红色对应于较低的减少量。该表面是使用截至 2022 年12月的数据计算的。

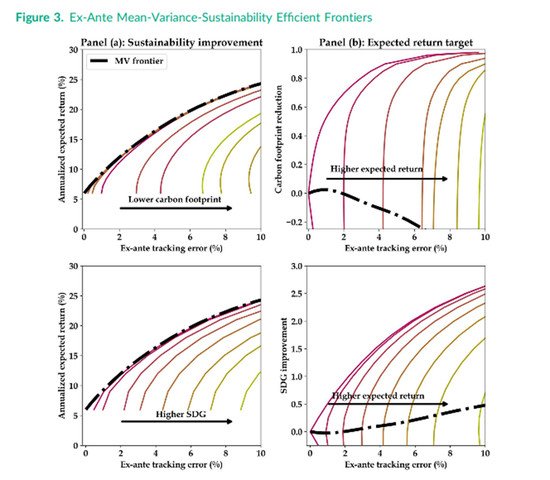
　　注：该图绘制了相对于基准的碳足迹减少（上）和可持续发展目标（SDG）改进（下）的事前预期回报-跟踪误差-可持续性边界。Panel（a）显示了改变投资组合可持续发展目标时的有效边界。Panel（b）在y轴上绘制了不同预期回报水平的可持续性衡量标准。这些图是使用截至 2022年12月的数据计算的。

　　因此，虽然我们提出的多目标优化框架是可推广在所有投资组合中的，但它对于希望实现雄心勃勃的可持续发展目标、且要求跟踪误差较低的投资组合尤其重要。因此，我们的实证将重点关注低跟踪误差投资组合。

　　4.2 减少碳足迹

　　投资组合的一个共同可持续发展目标是相对于某些基准减少碳足迹，目的是引导投资组合远离碳排放公司。实现这一目标的基本方法是强制执行投资组合约束，使得投资组合的碳足迹必须始终比基准好至少y%。虽然该方法将保证投资组合符合约束条件，但可能会导致性能不佳。约束方法实质意味着对预期回报征收随时间变化的碳税，因为当对碳足迹的约束变得更具约束力时，优化算法将对碳足迹较高的股票征收更高的“税”；参见 Blitz 和 Hoogteijling （2022）。因此，我们提议在目标函数中使用个股的碳足迹作为一种替代机制，以减少投资组合的整体碳足迹，同时综合考虑风险、预期回报与可持续性的三者平衡。这种方法对预期回报采取更稳定的碳税机制，并为预期回报与碳足迹减少的平衡提供更大空间。

　　为了评估这两种方法的实际影响，我们进行了一系列模拟，在这些模拟中，我们改变了选定的投资组合构建参数，以通过约束和优化方法探索对投资组合碳足迹的影响。我们运行了以下模拟：

　　1．         无约束模拟（表示为UC）；

　　2．         碳约束为y%的约束模拟（表示为Cy）；

　　3．         目标函数中加入碳变量的无约束模拟（表示为P）；

　　4．         目标函数中加入碳变量并碳约束为y%的约束模拟（表示为PCy）。

　　图4描绘了四种不同情景下投资组合相对于基准的碳足迹。UC模拟投资组合具有与基准相同的碳水平，考虑到投资组合的跟踪误差较低（0.5%），这是可预期的。碳约束为 0%（即等于或优于基准）的C0投资组合产生了与UC投资组合相近的结果，除了碳足迹始终低于基准。这一结果证明了投资组合碳足迹随时间变化的性质。该约束条件并不总是实际在约束投资组合，因此从预期回报的角度来看，实施起来相对“便宜”。这与C60（60%碳约束）形成鲜明对比，投资组合的碳暴露始终静态低于基准60%，因此该约束始终在起作用。最后，目标函数加入碳指标（3D）的情形中强调了投资组合如何随时间变化实现平均碳足迹减少60%。这样，投资组合优化可以更灵活地权衡碳足迹减少与风险和回报目标。

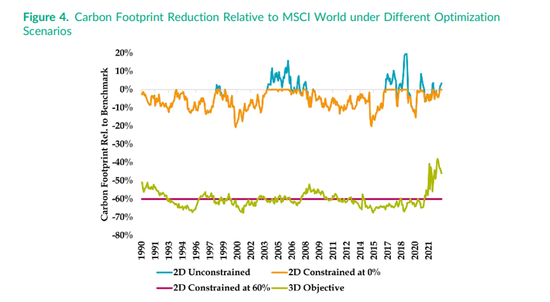
　　注：该图绘制了使用不同的 2D 和 3D 投资组合构建方法，投资组合碳足迹相对于 MSCI 世界碳足迹的改善百分比。我们报告的投资组合结果跟踪误差目标为 0.5%。

　　图 4 的结果也可以与当下经济现象联系起来。近年来，石油和天然气股票的价格势头强劲，但从估值角度来看仍存在低估，这从回报要素来看很有吸引力。因此，在3D投资方法下，优化组合会选择买入这些股票，从而导致投资组合的碳足迹增加。这与早期（例如 2012 年至 2020 年）形成鲜明对比，当时此类股票从回报要素角度来看相对没有吸引力，因此目标函数可以使投资组合的碳足迹减少幅度大于平均水平。

　　约束优化和3D投资方法之间的差异总体是由随时间变化的预期回报造成的。股票的碳足迹不会逐月发生显着变化，但预期回报预测可能会发生显著变化。因此，在每个月的重新平衡中，3D投资方法都会权衡预期回报和碳足迹。

　　表2列出了1989年12月至2022年12月期间的详细绩效统计数据。首先，我们注意到在A面板和B面板中，应用碳足迹减少作为约束条件的约束优化降低了其收益总体表现，从而降低了信息比率（Information Ratio，因为跟踪误差相对恒定）。其次，在两种情形下，3D 目标函数方法（P）均优于2D约束方法 （C60%/C75%）。3D目标函数方法提供了更高的总体表现和更低的调仓率，同时保持了可比的跟踪误差和碳足迹减少水平。这些结果反映在我们运行的跨越阿尔法回归6中，回归覆盖了我们前述提到的QMV、市值对数以及碳足迹得分等因素。在所有情形中对目标因素都有相同或基本等同的暴露，这突出了3D投资如何在保持相似因素暴露的同时，以更有效的方式纳入碳足迹目标。

　　【6】译者注：跨越阿尔法回归是一种用于评估投资组合表现的统计方法，特别是在量化投资和资产定价领域中。这种回归分析可以帮助投资者了解投资组合的收益是否能够被一组特定的风险因子所解释，以及投资组合经理是否能够通过选择特定的资产或因子来获得超出这些风险因子预期收益的超额收益（即阿尔法）。

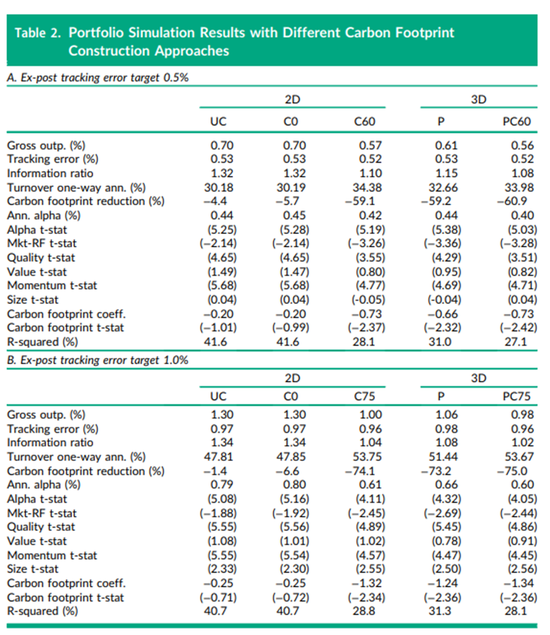
　　注：此表显示了完全投资的多头投资组合的绩效和跨度回归结果，该投资组合使用多因素预期回报目标、方差-协方差矩阵以及相对基准的碳足迹约束 （2D） 或直接在目标函数 （3D） 中纳入碳足迹目标进行优化。我们的样本从1989年12月到2022年12月，使用MSCI世界指数的成分股。投资组合每月重新平衡。面板（A）是跟踪误差为0.5%。面板（B）是跟踪误差为 1.0%。跨越回归将优化投资组合的总体表现回归到不同因素（质量、价值、动量、规模、碳足迹）的顶部减去底部投资组合的表现上。UC表示无约束。Cx表示比基准碳足迹低y%的约束。P表示将碳足迹目标纳入目标函数。PCy表示目标函数中纳入碳足迹目标，并加入了低于基准碳足迹y%的约束条件。R方是在排除可持续投资变量的回归中计算的。

　　我们还探索了目标函数方法和约束方法的结合。我们发现这种方法的效果不如孤立的方法，它比独立方法实现了更大的碳足迹减少，往往超出了目标减少水平。由于我们的碳减排目标较为严苛，因此任何增加都会对投资组合的总体表现产生重大影响。尽管如此，这样的组合凸显了如何确保目标减排水平，同时如果风险-回报-可持续性权衡适当的话，该方法可以使投资组合比目标约束做得更好。

　　我们将“2D Constraint”表示为目标是在某些碳足迹约束下最大化预期回报并最小化风险；我们也可以将跟踪误差作为约束，最大化预期回报和最低化碳足迹（2D TE Constraint）。在本文未报告的稳健性测试中，我们发现3D投资方法优于这种“2D TE Constraint”方法，“2D TE Constraint”方法优于“2D Constraint”方法。这表明，我们的3D投资方法通过将碳足迹项引入目标函数并允许这种权衡的发生而受益相对更多。

　　4.3 提高SDG得分

　　我们所提出框架的另一种应用是改善投资组合对可持续发展目标的正向衡量。我们使用 Robeco SDG分数，该分数用-3（差）到+3（优）来评判公司为联合国可持续发展目标做出的贡献。不同于碳足迹的负值，我们用SDG分数使目标函数中加入“奖励”或者将其视为“返税”，这会鼓励优化算法持有正SDG得分的股票。

　　图5显示了五种不同情形投资组合相对于基准的SDG目标得分，如图4所示。我们在这里发现了与“碳足迹减少”相似的结果。重要的是对于3D方法，我们观察到投资组合SDG分数在100%改进的约束平均值周围随时间变化。这一结果再次强调了针对可持续发展目标的3D目标函数方法的动态性质，而不是约束的固定性质。

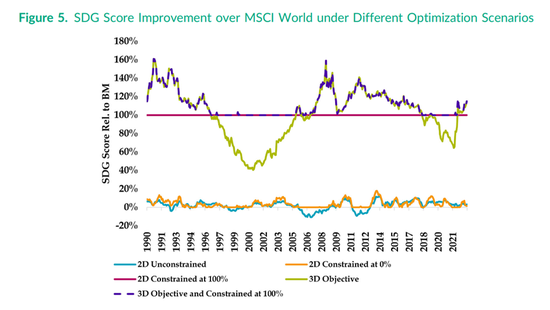
　　注：该图绘制了使用不同的 2D 和 3D 投资组合构建方法，投资组合的可持续发展目标 （SDG）分数相对于MSCI 全球SDG分数的改善百分比。跟踪误差为1.0%。

　　表3列出了1989年12月至2022年12月期间的详细表现统计数据。与表2相同，我们发现了与碳足迹情景中类似的定量结果。在面板A中，3D方法（P）在大多数指标上都优于约束方法（C70%）：更高的业绩表现（0.49%比0.46%）、更高的信息比率（0.98比0.88）以及更低的调仓率（26.7%对比31.4%）。在面板B中，1.0%跟踪误差，我们发现了同样可比结果，3D方法优于约束方法。

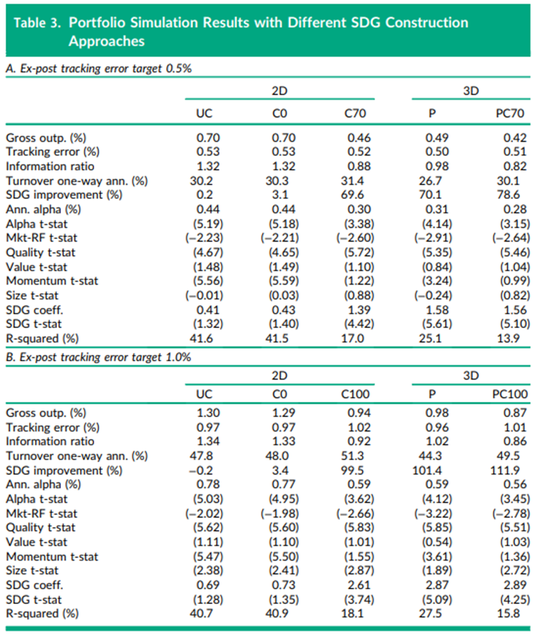
　　注：此表显示了使用多因素预期收益目标、方差-协方差矩阵以及基准相对SDG （2D）或直接在目标函数 （3D） 中的约束进行优化的完全投资的多头投资组合的绩效和跨度回归结果。我们的样本从1989年12月到2022年12月，使用MSCI世界指数的成分股。投资组合每月重新平衡。面板A是跟踪误差为0.5%的投资组合。面板B是跟踪误差为1.0%的投资组合。跨越回归将优化投资组合的总表现回归到不同因素（质量、价值、动量、规模、SDG）的顶部减去底部投资组合的表现之上。Cx表示比基准 SDG 分数高x%的约束。P表示SDG评分目标是目标函数中的一项。PCy表示SDG评分目标是目标函数中的一项且设定了高于基准SDG分数y%的约束。R方是在排除可持续投资变量的回归中计算的。

　　SDG=可持续发展目标；SI=可持续投资；UC=无约束。

　　05 影响和展望

　　5.1 不断发展的可持续发展数据的影响

　　通过上述两例，我们展示了在目标函数中加入可持续投资指标，通常优于简单地在投资组合层面施加固定约束。3D投资框架可推广到任何可以表示为离散或连续序列（序数）的可持续性指标。实证对应于投资管理中常见的可持续性衡量标准，我们观察到如何根据衡量标准本身（结合使用的预期回报和风险模型）产生结构上不同的结果。为此，更广泛的问题仍然存在：构建满足未来可持续发展愿望的投资组合的最佳方式是什么？图 6 显示了随时间变化的MSCI全球基准的市值加权碳足迹、ESG和SDG得分。基准可持续性得分随时间变化，但它并不总是朝一个方向发展。这些变化对于如何构建针对这些措施的投资组合具有重大影响。

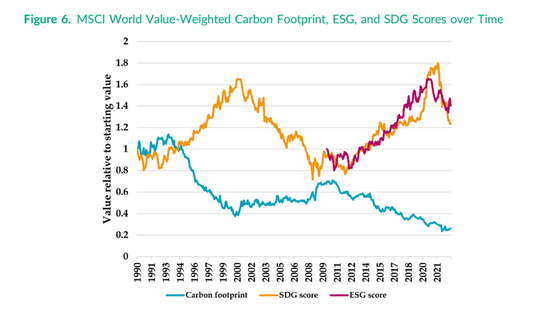
　　注：该图绘制了MSCI全球基准的市值加权碳足迹、可持续发展目标 （SDG） 得分以及环境、社会和公司治理 （ESG） 得分。碳足迹和SDG的样本从1989年12月到2022年12月。ESG的样本从2009年12月到2022年12月。每个序列的各项值均为当前值与时间序列中第一个值的比率。

　　随着平均基准分数从2015年到2022年有所增加，MSCI ESG分数相对于基准的改善变得越来越具有挑战性。严格来说，问题不在于基准分数的增加，而在于分数上限是10.0的ESG评分，分布偏斜且集中。例如，假设基准分数为8.0，期望改善20%，对应投资组合的ESG得分应为9.6，这就需要持有大量ESG得分为10.0的股票。因此，投资组合构建将在很大程度上受到ESG评分的推动，而预期回报和风险则成为次要因素。通过使用目标函数方法，此类基准变化的影响可以相对可控，并且优化算法将能够更好地权衡预期回报、风险和可持续性目标。但是，在这两种情况下，所选择的度量标准还是对优化算法有相当大的影响，因此，在确定投资组合优化算法中的目标时，选择理想的度量标准非常重要。

　　5.2 如何在不同方法中选择

　　投资组合约束是确保遵守可持续发展目标的最常见方法。确保投资组合可持续性、合规性的另一种流行方法是通过全域排除，例如排除所有被视为“罪恶股票”的名称。本文验证了3D 投资是可以提高投资组合可持续性目标的有效方法，提供帕累托最优和更大的灵活性。然而，这一结果并不意味着传统的基于约束和排除的方法没有优点并且应该被抛弃。

　　当投资者希望始终实现投资组合层面的可持续性目标时，基于约束的投资组合方法是合适的。同样，基于排除的方法可以确保始终实现个股级别的可持续性目标。这是因为约束和排除是硬性标准，因此，投资组合优化必须满足所有拟议投资组合的这些目标。另一方面，本文讨论的3D投资方法代表了一种软标准。它更加灵活，因为它使投资组合能够在可持续性、风险和预期回报之间进行权衡。与不具有可持续性目标的投资组合相比，这种权衡确保了更加卓越的可持续性目标实现，但它并不能保证在任何给定时间点都满足特定的可持续性目标。

　　这些硬约束和软约束在投资组合构建中都有各自的用例。如果想要始终确保一定程度的可持续发展目标水平或确保某些名称不会出现在投资组合中，则应分别使用约束和排除。另一方面，如果投资经理想要实现更好的平均可持续性发展目标，但当条件合适时，可能会追求更高的预期回报，那么3D优化方法是合适的。例如，当石油和天然气公司的价格如此低廉以至于其预期回报非常高时，基于优化的方法允许暂时牺牲可持续性以获得更高的预期回报。

　　最后，随着欧洲绿色新政等新监管的发展，将收益、风险以外的目标纳入投资范式的必要性将继续增长。我们的方法提供了一个与监管环境兼容的框架，使投资者能够围绕可持续性目标的整合以及明确的风险和回报考虑因素做出更透明的决策。我们框架的核心是股票选择模型（Stock-selection Model）——选择具有最高预期回报的股票。这仍然是投资范式的前沿和中心，我们的框架允许采用更灵活的方法来纳入可持续发展等目标。

　　06 结论

　　投资历来是一项多维度的工作，但投资组合构建方法通常被认为是二维的。可持续投资是众多多目标投资的最新例子。我们展示的3D投资框架，在同时考虑两个以上投资目标时产生“最佳可能”的解决方案。历史模拟凸显了这种方法相对于传统的约束性可持续投资方法的优越性（减少碳足迹和获得更高的SDG分数）。与纯粹基于约束的方法相比，3D 投资平均可以实现更高的可持续性特征和预期回报。

　　值得注意的是，限制因素在可持续投资中并非没有用处。在实践中，可能会首选混合方法——将合理的可持续性约束条件和3D目标函数相结合。这种方法保证了基本水平的可持续性目标，同时允许优化算法在回报、风险和可持续性之间进行机会主义权衡。如果希望实现比较激进的可持续性目标，那么3D投资方法是最理想的，这种方法将可持续性与阿尔法和风险一起明确地作为目标。

　　结束

　　Financial Analysts Journal（简称”FAJ”） 是CFA协会（CFA Institute）主办的全球知名的投资管理领域专业期刊，该刊为季刊，每期发表论文4-8篇，在社会科学引文索引（SSCI）位列二区。

　　2021年底，CFA北京协会获得了CFA Institute期刊编辑部正式授权，邀请了一批协会内外的专家和志愿者作为推荐人/审校人，启动了FAJ研究成果推广项目。

　　【项目使命】本项目定位于将期刊的优秀研究成果，尤其是对中国投资实践具有启发意义的研究成果，以中文推荐和综述的形式发布在包括不限于“北京金融分析师协会”公众号的公共平台。项目的推荐人均为在金融投资实践和学术研究方面具有一定经验和成果的专业人士，因而能够较好的将来自国际市场的学术研究成果进行中国本土化转化，揭示出对我国金融市场的学习借鉴意义，吸收国际前沿学术成果，使之融入我国金融业的高质量发展和双向对外开放历史进程。

　　截至2024年12月初，本项目已经发布研究成果50期，涉及资产配置理论前沿、ESG投资理论与实践、市场微观结构、组合构建策略、行为金融等多个领域，据不完全统计，这些研究成果的全媒体累计阅读量超过123万人次，公众号累计分享次数超4700次，包括中国人民银行主管的《金融时报》新媒体平台、财新网、新浪、凤凰等传统门户、清华金融评论、学说等学术类新媒体平台、中国保险资管业协会等行业组织公众号，都对本项目的研究成果多次关注和转载。

　　2024年6月5日，CFA北京协会FAJ中文推介项目作为“协会成功故事”被CFA Institute官方网站Connexions报道，分享给全球160余家CFA地方协会。